LFR论文速读(ICLR, 2024)
LFR(ICLR, 2024),有源码
自监督表示学习基于变换不变性假设,使用人工设计的数据增广策略获得了极大提升,但是提升主要集中于视觉和自然语言处理领域,在其他数据模态中并没有直接的应用,甚至可能与特定应用的数据增强约束相悖(application-specific data augmentation constraints: 部分任务不能应用所有增广策略,例如医学图像处理不能左右翻转或者随意改变色彩)。这篇文章展示了一个可被用于任何模态的SSRL(Self-supervised representation learning)策略,因为这种方法并不进行任何增广或者掩码。特别的,它证明高质量的数据表征可以通过重构随机的数据投影获取。作者在一系列表示学习任务上评价了这种方法,发现其优于多个SSRL的SOTA。
要点速递
- E-M法更新模型:依次更新主干网络和分类头网络,并且更新次数不相同,让分类头充分训练可以让其充分发挥主干网络提取表示的能力。
- batch-wise Barlow Twins:让同一个样本的不同增强版本在特征空间中尽可能相似(invariant),同时鼓励特征向量的不同维度之间不冗余(decorrelation)。在这篇文献中就是让相同样本经过随机投影和预测头后得到结果尽量接近,而让不同样本尽量远离。
- 随机映射器的选择:使用Fast DPP选择多个映射器,将映射器输出的batch展平并组装为方阵,计算其行列式(det),越大代表不同映射器差别越大。
Introduction
这篇文章的激发点来自于一个传统的思考:一个好的表示应该可以用于大量的下游任务中,尤其是一部分下游任务中可能有随意的数据映射。
正式的说,$G = {\dots g^{(k)}(\mathrm{x})\dots}$是一个随机的从原始特征出发的映射函数。上述的激发点代表着有一个好的表示$\mathrm{z}$可以通过简单的函数$H= {\dots h^{(k)}(\mathrm{z})\dots}$预测上面的随机映射。
通过这种思考,表示学习可被构建为对于嵌入$\mathrm{z}$和预测函数$H$的搜索,这里的嵌入和预测函数需要能预测随机数据映射的结果。
Architecture
原数据$X={\dots \mathrm{x}_{i}\dots}$,每个点都共享一个特征域$\mathcal{X}$,表示学习的工作是学到一个$f_{\theta}(\mathcal{X})$来产生低维度的嵌入$\mathrm{z}\in \mathcal{Z}$。该表示必须带有足够的信息,这样在下游任务$g(\mathcal{X})$中才能有效学习一个简单的预测函数$h_{\phi}(\mathcal{Z})$来使用$h_{\phi}(f_{\theta}(\mathrm{x_{i}}))$复制$g(\mathrm{x_{i}})$
前置任务:随机的多目标学习
作者并不清楚对于随机选取的任务是否能提取有效的表示,所以他做了个实验:
前置任务可以分为三个组件:1. 一个表示模型; 2. 一组随机产生的数据映射函数$G={\dots g^{(k)}(\mathcal{X})\dots}$; 3. 一系列简单的预测头$H_{\phi}={\dots h_{\phi }^{(k)}(\mathcal{Z}),\dots}$。作者如下描述优化目标:
$$
\underset{\theta, \Phi}{\operatorname{argmin}} \sum_{\mathbf{x}_{i} \in \mathcal{X}} \sum_{k} \mathcal{D}\left[g^{(k)}\left(\mathbf{x}_{i}\right), h_{\phi}^{(k)}\left(f_{\theta}\left(\mathbf{x}_{i}\right)\right)\right]+\lambda_{1} \Omega_{1}(\theta)+\lambda_{2} \Omega_{2}(\Phi)
$$
其中$\mathcal{D}[\cdot,\cdot]$是一个散度度量,用于计算输入的相似性。$\Omega(\cdot)$是正则项,为了让这个任务变得不是那么显然,预测器不会太复杂,所以只会是一个线性层或者简单的神经网络。
$$
\begin{array}{l}\sum_{i} \log p\left(Y_{i} \mid \mathbf{x}_{i}\right)=\sum_{i} \sum_{k} \log \int_{\mathbf{z}_{i}} p\left(\mathbf{y}_{i}^{(k)} \mid \mathbf{z}_{i}\right) p\left(\mathbf{z}_{i} \mid \mathbf{x}_{i}\right) d \mathbf{z}_{i} \\ \quad \geq \sum_{i} \sum_{k} \int_{\mathbf{z}_{i}} p\left(\mathbf{z}_{i} \mid \mathbf{x}_{i}\right) \log p\left(\mathbf{y}_{i}^{(k)} \mid \mathbf{z}_{i}\right) d \mathbf{z}_{i}=\sum_{i} \sum_{k} \log p\left(\mathbf{y}_{i}^{(k)} \mid \mathbf{z}_{i}=f_{\theta}\left(\mathbf{x}_{i}\right)\right),\end{array}
$$这里的推导用到了边缘化z变量,然后利用Jensen不等式得到下界$\log \mathbb{E}[f(Z)] \geq \mathbb{E}[\log f(Z)]$->$\log \mathbb{E}_{z\sim p(z|x_{i})}[p(y_{i}^{(k)}|z_{i})]\geq \mathbb{E}_{z\sim p(z|x_{i})}[\log p(y_{i}^{(k)}|z_{i})]$
这里的$p(\mathrm{z}_{i}|\mathrm{x}_{i})$是一个Dirac delta分布,因为表示模型是一个确定性函数(就是给定了x就确定了z,所以这里其实是一个在某个值为1,其他均为0的概率函数)。当$p(\mathbf{y}_{i}^{(k)} \mid \mathbf{z}_{i})$是一个高斯函数,则对应的$\mathcal{D}$就是欧几里得距离。
对于优化目标,最简单的训练方法就是同时训练表示模型和预测器。但是实际测试下来效果并不好。
于是作者使用EM算法来解决训练不稳定的问题。鉴于MLE的下界,优化表示函数为E步,在给定的对数似然估计模块上估计后验概率,对于M步,表示函数为固定的,我们优化预测头,这里作者如下训练SSRL模型:
E-Step
$$
\underset{\theta}{\operatorname{argmin}} \sum_{i} \sum_{k} \mathcal{D}\left[g^{(k)}\left(\mathbf{x}_{i}\right), h_{\phi}^{(k)}\left(f_{\theta}\left(\mathbf{x}_{i}\right)\right)\right]+\lambda_{1} \Omega_{1}(\theta)
$$
M-Step
$$
\underset{\Phi}{\operatorname{argmin}} \sum_{i} \sum_{k} \mathcal{D}\left[g^{(k)}\left(\mathbf{x}_{i}\right), h_{\phi}^{(k)}\left(f_{\theta}\left(\mathbf{x}_{i}\right)\right)\right]+\lambda_{2} \Omega_{2}(\Phi)
$$
优化预测模型的轮数大于优化表示模型,这让预测模型更加接近其在给定表示模型时最佳的表现。
散度度量:batch-wise Barlow Twins
Barlow Twins是 2021 年由 Facebook AI 提出的无监督对比学习方法,目标是学习一个信息丰富且非冗余的表示向量。核心思想是:
让同一个样本的不同增强版本在特征空间中尽可能相似(invariant),同时鼓励特征向量的不同维度之间不冗余(decorrelation)。
这里作者使用Barlow Twins的原因是:MSE会降低小错误的重要性权重、CE不适合于回归任务、对比和三重损失会大大引入随机性。而Barlow Twins则可以有效通过减少冗余的方法获得高质量的表示。其损失函数可以描述如下:
$$
\mathcal{L}_{\mathrm{BBT}}=\sum_{k} \sum_{i}\left[\left(1-c_{i i}^{(k)}\right)^{2}+\lambda \sum_{j \neq i} c_{i j}^{(k)^{2}}\right]
$$
其中$c_{ij}$为余弦相似度矩阵中的元素。
$$
c_{i j}^{(k)}=\frac{\mathbf{y}_{i}^{(k)^{\top}} \hat{\mathbf{y}}_{j}^{(k)}}{\left|\mathbf{y}_{i}^{(k)}\right|_{2}\left|\hat{\mathbf{y}}_{j}^{(k)}\right|_{2}}, \quad \mathbf{y}_{i}^{(k)}=g^{(k)}\left(\mathbf{x}_{i}\right), \quad \hat{\mathbf{y}}_{i}^{(k)}=h_{\phi}^{(k)}\left(f_{\theta}\left(\mathbf{x}_{i}\right)\right)
$$
其中$\mathbf{y}_{i}^{(k)}, \hat{\mathbf{y}}_{i}^{(k)}\in \mathbb{R}^{d^{(k)}}$,这里为什么标签会有多个维度呢,我去看了代码,这里的标签是直接由模型最后一层输出的结果,下一步就是取softmax并找出最大值。所以当有d个类时,就有d个维度。k代表k个映射器或预测头,i代表的是样本编号,m代表batch-size.
随机数据映射器的多样性鼓励
随机数据映射器构造出的数据训练出的模型可能有大量相似的信息,为了提高数据映射器的多样性,作者提出从$N\gg K$个随机生成的映射器中选取K个。该理论基础是:一个足够大的数据集可以揭示不同随机映射器的不同点。假设这里有一组数据$X\in \mathbb{R}^{m\times d}$。对于每个随机映射器,我们可以产生如下归一化的输出:
$$
Y^{(k)}=g^{(k)}(X) /\left|g^{(k)}(X)\right|_{2}, \quad Y^{(k)} \in \mathbb{R}^{m \times d^{(k)}}
$$
然后对每个映射器计算输出的余弦相似度
$$
A^{(k)}=Y^{(k)}\left(Y^{(k)}\right)^{\top}, \quad A^{(k)} \in \mathbb{R}^{m \times m}
$$
通过将矩阵$A^{(k)}$展平并再次归一化,获得一个向量$\mathbf{a}^{(k)}\in \mathbb{R}^{m^2 +1}$,这个向量作为第k个映射器在该批次上的印迹(? signature并不是那么好翻译)。最后,我们将从N个候选者中选择K个模型,选择策略如下:
$$
\underset{\mathbf{s}}{\operatorname{argmax}}|\operatorname{det}(B)| \quad
\quad B=\tilde{A} \tilde{A}^{\top}, \quad \tilde{A}=\left[\mathbf{a}^{(k)} \mid k \in[0, N], s_{k}=1, \sum_{k^{\prime}} s_{k^{\prime}}=K\right]
$$
是一个组合优化问题,其目标是:从所有投影器中选择 K 个,使得它们所构成的特征矩阵的“结构尽可能丰富、互相独立”。这个问题可以使用一些近似方法解决(Fast DPP)
Experiment and Evaluation
Datasets
作者选用多种数据集,包括时间序列、表格数据和计算机视觉。这里我们主要关注三个:1. 表格数据作者使用了Adult Income(binary), First Order Theorem Proving(6-class classification), HEPMASS(binary); 2. 计算机视觉中作者使用了一个消化道照片的数据集; 3. 时间序列中有一个MIMIC-III数据集,其为标准的电子病历时间序列。
Implementation
Evaluation
MIMIC-III使用MLP分类器,表格数据使用逻辑斯蒂回归作为分类器,其余数据集均采用线性分类器。作者在训练集上训练分类器(固定表示层),测试集上评估性能
Model Architectures
MIMIC-III数据集,我们使用Temporal Convolutional Network(时间卷积网络),表格数据使用4层MLPs
Baseline

表 1 总结了我们实验中使用的所有基线方法。值得注意的是,虽然我们提出的框架 LFR 是领域无关的(domain-agnostic),但一些流行的自监督表示学习(SSRL)方法,例如 SimCLR 和 SimSiam,需要针对特定领域的数据增强策略以达到最佳性能。具体来说,SimCLR 和 SimSiam 默认用于生成视图(view)的增强方法是为自然图像分类设计的,可能不适用于其他类型的数据模态。在我们对表格数据集的实验中,我们将我们的方法与 SCARF(Bahri 等人, 2022)进行比较。SCARF 是一种针对表格数据调整后的 SimCLR 版本,它使用随机扰动(random corruptions)作为增强方法。
Performance
我们的实验表明,对于那些没有标准化增广策略的模态,例如医学影像、时间序列和表格数据,LFR 在自监督表示学习(SSRL)方法中表现最强,在大多数情况下超过了其他自监督学习方法,包括一些领域无关的方法(如 DACL)。例如,在 HAR 和 Epilepsy 数据集上,LFR 是表现最好的方法,甚至超过了针对时间序列设计的自监督学习方法 TS-TCC。同样地,对于 Income 和 Theorem 数据集,LFR 的表现优于针对表格数据的自监督学习基线方法 SCARF 和 STab。虽然在 HEPMASS 数据集上 LFR 并非最佳,但仍然表现良好,与自编码器(autoencoder)和 SCARF 相当。有趣的是,在 Income 数据集上,LFR 的表现甚至超过了监督训练。
对于时间序列和表格数据,基于增强的方法(如 SimSiam)往往表现不佳。例如,在 HAR 和 Income 数据集中,SimSiam 的表现甚至不如随机初始化的编码器。
这一实验结果验证了我们的假设——通过预测随机数据投影,有可能学习到高质量的数据表示。LFR 在那些难以构建语义保持增强(semantic-preserving augmentation)的领域中表现相对较好。
Performance on Medical Applications
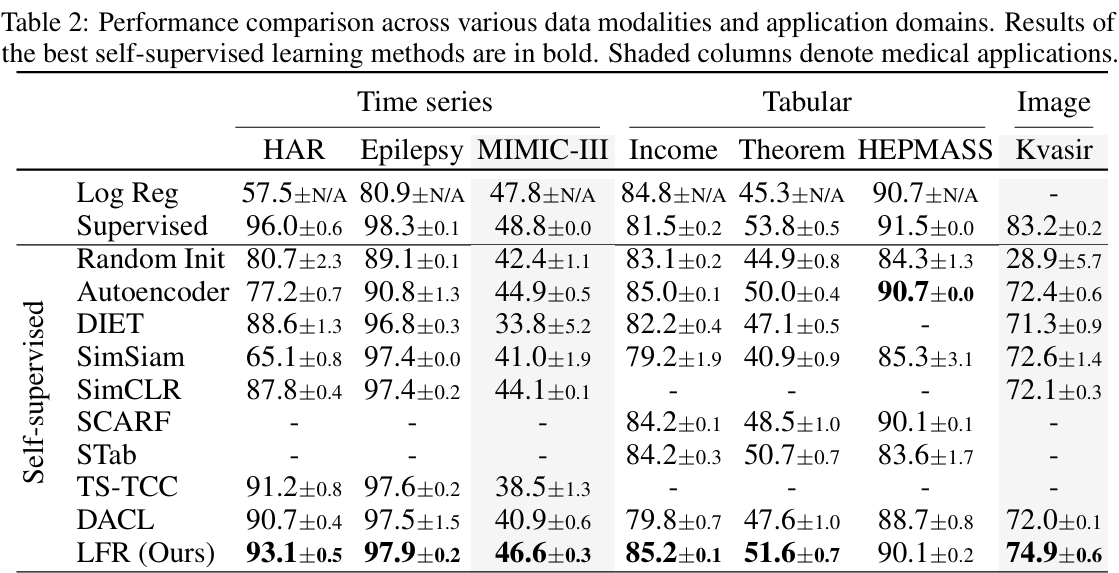
为了比较医学领域内LFR的效果,作者使用了两个医学数据集进行比较,Kvasir和MIMIC-III。在Kvasir上表现最佳,在MIMIC-III表现优良。主要是目前已有的增广策略并不适合医学影像,LFR是对于医学影像深度学习的有效方法。
Impact of Random Data Projection Diversity
作者对于随机映射器的选取使用了Fast DPP,初始化使用了两种方法:Beta 初始化和权重Dropout.
Beta initialization
一种卷积层权重初始化方法。核心思想:让卷积核在训练开始时就对不同方向的边缘敏感,而不是随机初始化,这有助于更快收敛或学习更稳定的特征。
作者使用$\text{Beta}(\alpha,\beta)$其中$\alpha=0.5,\beta=0.5$初始化
Dropout initialization
做法:在初始化权重后,随机将40%(corruption rate = 0.4)的权重置为0,然后冻结权重,不再训练
Result
两种方法并用效果最佳。
Ablation Study
Number of projectors
当映射头数目为6时效果最佳
过多的映射头可能带来冗余的特征,进而造成偏倚。
Batch size
256最佳,但是图上显示其实没有显著性(64-128-256-512).
Predictor epochs
7轮训练最佳。
Embedding dimension
2048以后,上升趋势变缓,所以选择2048维。
Conclusion
本文提出了一种新颖的 自监督表示学习(Self-Supervised Representation Learning, SSRL)框架,它既与数据模态无关,也与应用场景无关。我们提出的框架利用随机投影(random projectors)从未标注的数据中学习表示,在各种模态和应用中均表现出色,尤其适用于那些尚未建立稳健增强流程的情境。
LFR 技术最适合无法对数据进行合理增强的情况(例如缺乏领域知识时)。虽然这一情况看似令人意外,但在一些关键应用领域(如医疗健康)中却非常常见。对于一般应用,如果对应用领域有充分理解,并能够合理设计增强策略,那么基于对比学习的自监督方法仍可能优于随机投影方法。总体而言,我们将 LFR 视为对 SSRL 文献的有益补充,用于填补无需数据增强的自监督学习方法的空白,以满足许多关键应用的需求。
虽然 LFR 鼓励在不同模态和领域中使用自监督学习而无需专家知识设计增强策略,但由于学习过程中人类干预有限,可能增加敏感特征被误用的风险,从而带来隐私或公平性问题。我们建议在使用自监督方法时进行人工监督,以确保数据的适当使用。
