GNN
图是我们身边非常常见的结构,最近的一些研究让我们能够使用图结构的优势,在许多领域,如抗生素的研究、物理仿真、虚假新闻的识别,交通预测和推荐系统都有了最新的研究与实践。
这篇学习/总结博客参考了biliili上李沐的带读以及A Gentle Introduction to GNN
这篇文章探索并解释了现代图神经网络,我们将工作分为4个部分:1. 什么类型的数据可以以图的形式记录;2. 图结构的特点与优势:相较于CNN或者传统深层神经网络;3. 建造一个GNN模型:从一个骨架到SOTA;4. 提供一个GNN playground供读者探究(会超链接回原文章)。
What a Graph is
图是一系列实体之间的关系
如果我们用图论的知识来看,图的描述其实有多种方式,如:邻接矩阵、集合的表示。我们这里采用相对容易接受的集合表示方法:
一个图主要由 节点(Nodes) 和 边(Edges) 构成。以下图为例:其中存在5个节点,与6条边。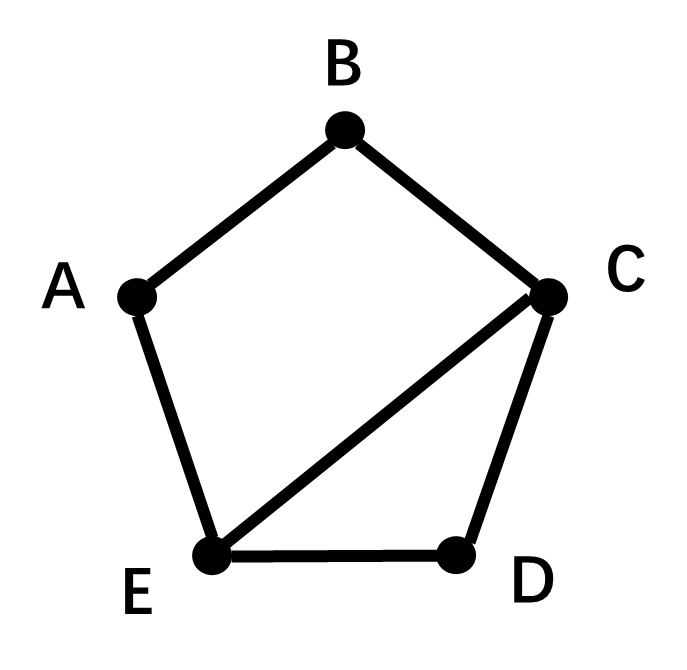
其中点集合为$V = { A,B,C,D,E }$。边集合为$E = { AB, BC,CD,DE,AE, CE }$上图边为无向的,所以也被称为无向图(有向图); 又因为没有重复边,所以被称为简单图;上图可以通过集合套集合的方法表示,即$G= { V,E }$
由于篇幅问题,我们仅仅引入简单的概念,图论是一个非常庞大的研究方向,如果对图论与图相关算法感兴趣,可以查看图论相关博客
GNN中的图
有趣的是,在GNN中,每个节点与边并不是我们想象的用单个数字代表其权重,而是通常由一个向量表示,我们称其为embedding(嵌入)
此外,在V,E之外,还有一个全局嵌入(U),其表示的是图中的边数与点数。
可以转化为图的数据
- 化学分子
- 图像(像素为节点)
- 文本(词语为节点)
- 社交网络
图解决的问题
图层面
寻找图中的环
点层面
将一个图分为两张图
边层面
学习社交网络中的关系(关系抽取)
GNN
GNN是对图上所有的属性(边、点、全局属性)进行可优化的变换,这个变换依旧保持图的对称性。”graph-in, graph-out”输入是图,输出是图,修改图的属性但是不影响图片的联通性(不影响结构)
最简单的GNN
对于点、边、全局向量输入MLP得出新的点、边、全局变量
例如:判断图中顶点属于1还是属于2,就是对于顶点中每个点的向量输入MLP并输出一个softmax的结果:1 or 2
如果点、边向量不存在,则需要通过pooling(池化?)来根据该点的附近点、边向量获得该点的向量。
信息传递
但是,我们很容易就会发现,这样的GNN对于图信息的利用效率其实是很低的:我们没有用到图中点与点之间的关系,而是简单的用3个独立MLP进行了向量的更新。
所以我们提出了信息传递的思路
- 最简单的信息传递就是汇聚,将一个点的向量和与其相连的所有点的向量相加后再输入MLP内进行更新,这样就可以用到点的邻接关系了。类似于卷积操作,但是这里的卷积权重均为1,且每次卷积就是对于每个点进行求和
- 那我们考虑,能不能把边的信息也纳入其中?所以可以首先把顶点的向量传入边,然后再把边的信息传入点。
- 但是到现在都没有用到全局信息,为了使用全局信息,我们会加入一个master node(context vector),这就是U,其与所有边和点相连。所以在更新点与边的时候,会利用到U;同时,在更新U的时候也会使用边与点的信息。
