二项分布与poisson分布及其应用

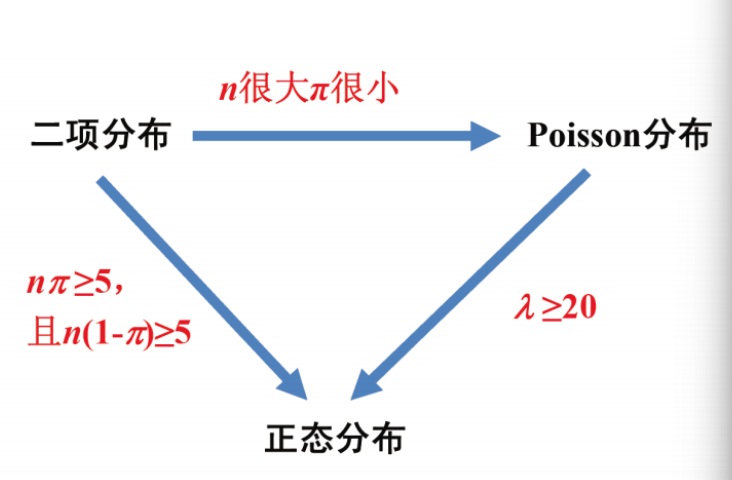
二项分布

$$ P(X) = C^x_{n} \pi^x (1-\pi)^{n-x}$$ $$\mu = n\pi, \sigma^2={ n\pi(1-\pi) }$$

样本率的方差计算同正态分布时的均值的方差计算：
$$S_{p}=\sqrt{ \frac{p(1-p)}{n} }$$
总体率置信区间计算：

  1. 查表方法
  2. 正态近似法(样本容量>100, $\pi \approx 0.5$)
$$\begin{aligned} u &= \frac{{p-\pi_{0}}}{\sigma_{p}} \\ \sigma_{p} &= \sqrt{ \frac{\pi_{0}(1-\pi_{0})}{n} } \end{aligned}$$ *既往死亡率为40%，实验中120名病人死亡30名，统计推断： H_0: 均值不等 H_1: 均值相等 确定alpha值为0.05，双尾检验* $$\begin{aligned} \sigma_{p}&=\sqrt{ \frac{\pi_{0}(1-\pi_{0})}{n} }\\ &=\sqrt{ \frac{0.4(1-0.4)}{120} }\\ &\approx 0.045\\ u&=\frac{{p-\pi_{0}}}{\sigma_{p}}\\ &=\frac{{\frac{30}{120} - 0.4}}{0.045}\\ &=-3.333 \end{aligned} $$

显著：拒绝H_0，因为超过了3个标准差

Poisson分布

$$P(X)= \frac{\lambda^x}{x!}e^{-\lambda}, X=0,1,2,\dots$$
$$\mu=\lambda, \sigma^2=\lambda$$
总体率置信区间计算：

  1. 查表方法
  2. 正态近似法($\mu \approx 0.5$)
    分布间关系

RR值和OR值的估计

RR值适用于：队列研究(risk ratio)
OR值适用于：病例对照研究(odds ratio)

指标 全称 定义 适用研究
RR 相对危险度（Relative Risk） 暴露组患病概率 / 非暴露组患病概率 队列研究（可以“跟踪”发病）
OR 比值比（Odds Ratio） 病例组的暴露几率 / 对照组的暴露几率 病例对照研究（不能计算发病率）

为何适用于不同研究类型？

队列研究 → RR

  • 从“暴露”开始观察，可以得到真正的“发病概率”。
  • 所以可以直接算：
    $$RR = \frac{P(\text{发病}|\text{暴露})}{P(\text{发病}|\text{非暴露})}$$​

病例对照研究 → OR

  • 从“疾病状态”出发选人（先有病例和对照），无法算发病率。
  • 只能算暴露与非暴露的“比值”：
    $$OR = \frac{\text{病例组中暴露/非暴露}}{\text{对照组中暴露/非暴露}}$$

生存分析 → HR(harzard ratio)

  • 定义：HR 衡量暴露组相对于非暴露组在 随时间变化的事件发生速率（例如生存分析中的死亡率、疾病发生率等）的比率。它通常用于 生存分析，尤其是 Cox比例风险模型 中。

  • 计算方法：HR 基于时间的事件发生风险计算，可以理解为暴露组和非暴露组在单位时间内发生事件的风险比：
    $$HR = \frac{\text{暴露组事件发生率}}{\text{非暴露组事件发生率}}$$

    它考虑了随时间推移的风险，而不仅仅是单纯的事件发生与否。

举个例子

发病 未发病 总计
暴露组 30 70 100
非暴露组 10 90 100
总计 40 160 200
$$\begin{aligned} RR &= \frac{\frac{30}{100}}{\frac{10}{100}}=3 \\ OR &= \frac{\frac{30}{10}}{\frac{70}{90}}=3.86 \end{aligned}$$

口诀： “RR 看未来，OR 看过去”

  • RR 是“先暴露后观察结果” → 队列研究
  • OR 是“先有病例找原因” → 病例对照

卡方检验

理论频数的计算：

有效 无效 总数 概率
A组 68(74*87.59%) 6 74 91.89%
B组 52 11 63 82.54%
总计 120 17 137 87.59%

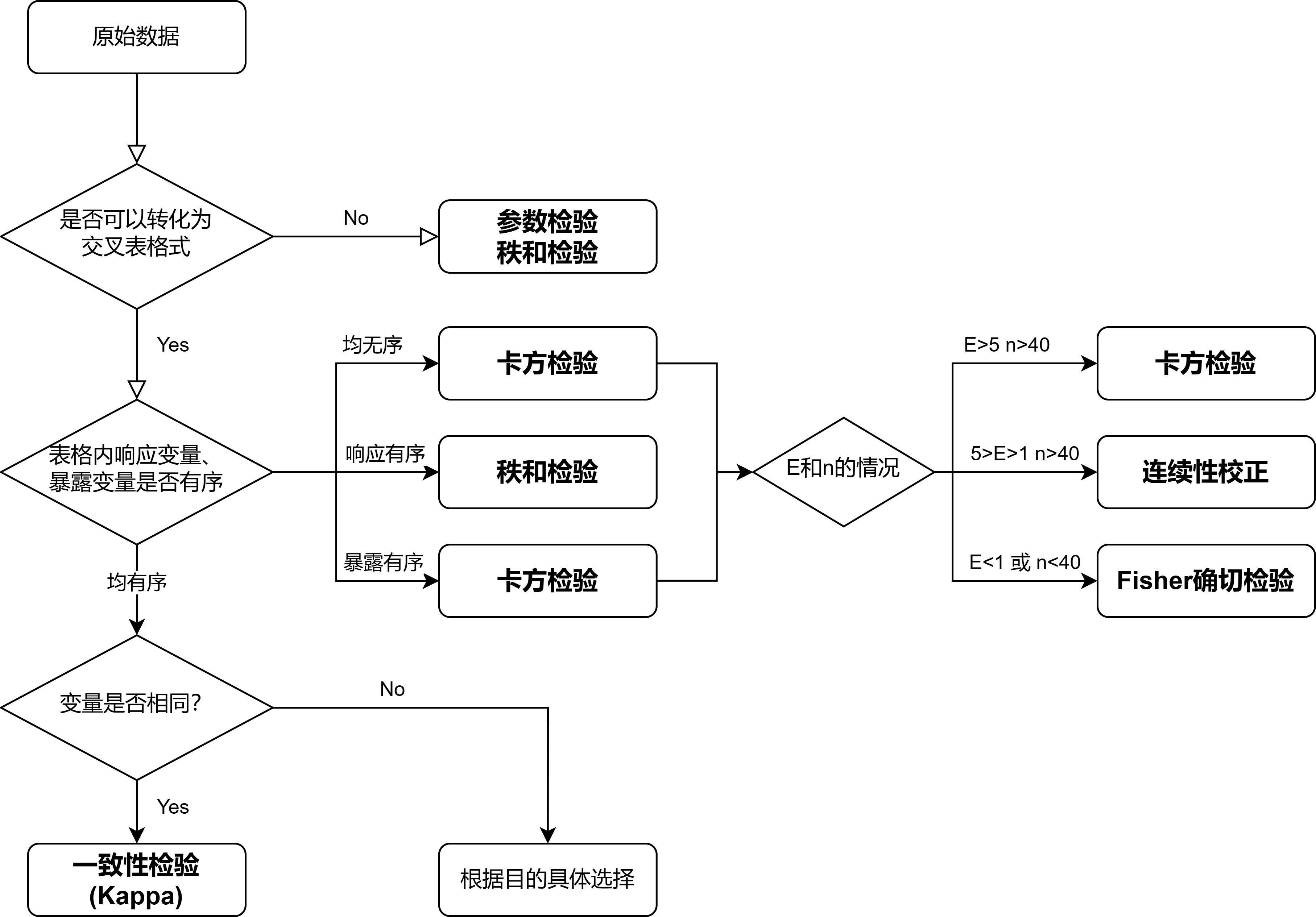
普通卡方：$n\geq40, E\geq5$
连续性校正卡方：$n\geq40, 1\leq E\leq5$
Fisher确切检验：$n\leq40$ 或 $E\leq {1}$

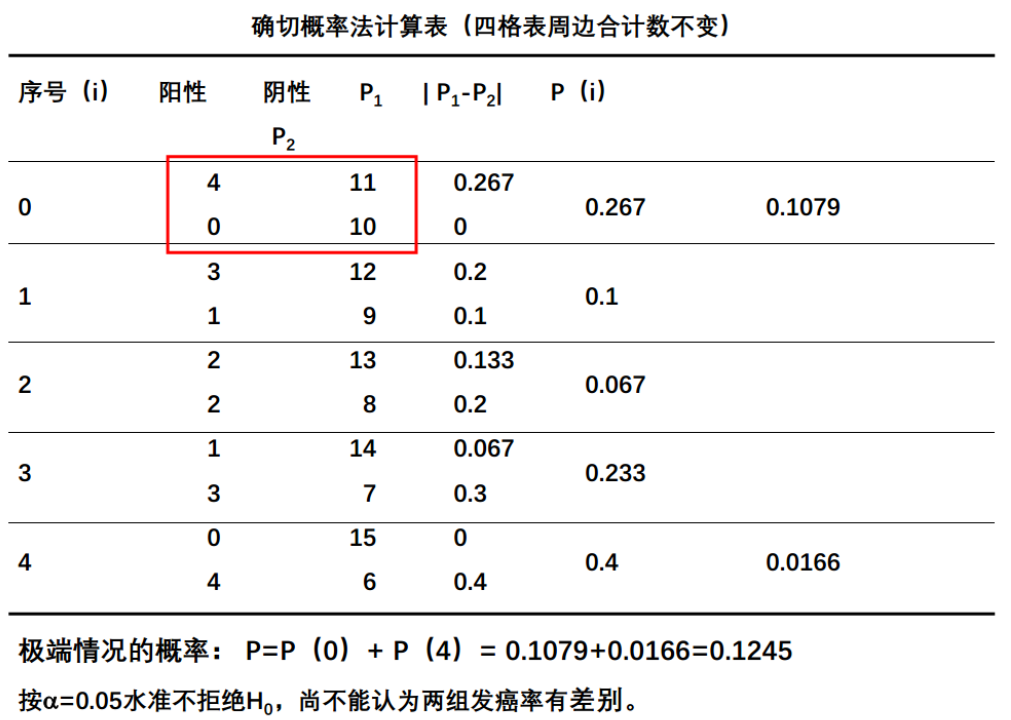
例题：15只4只发生癌变，对照组10只0只癌变

癌变 未癌变
暴露组 4 11
非暴露组 0 10

卡方检验实例

配对卡方检验

行列表卡方检验

  1. 多个率的比较
  2. 率的多重比较
  3. 多个构成比的比较
  4. 两种属性关联性检验

多种R $\times$ C表资料统计分析方法

卡方检验

  1. 双向无序
  2. 单向有序：组别有序、结果无序

秩和检验

  1. 单向有序：组别无序、结果有序

拟合优度的卡方检验

  1. 单变量
  2. 二项分布
  3. Poisson分布

卡方检验

Cover image icon by Freepik from Flaticon