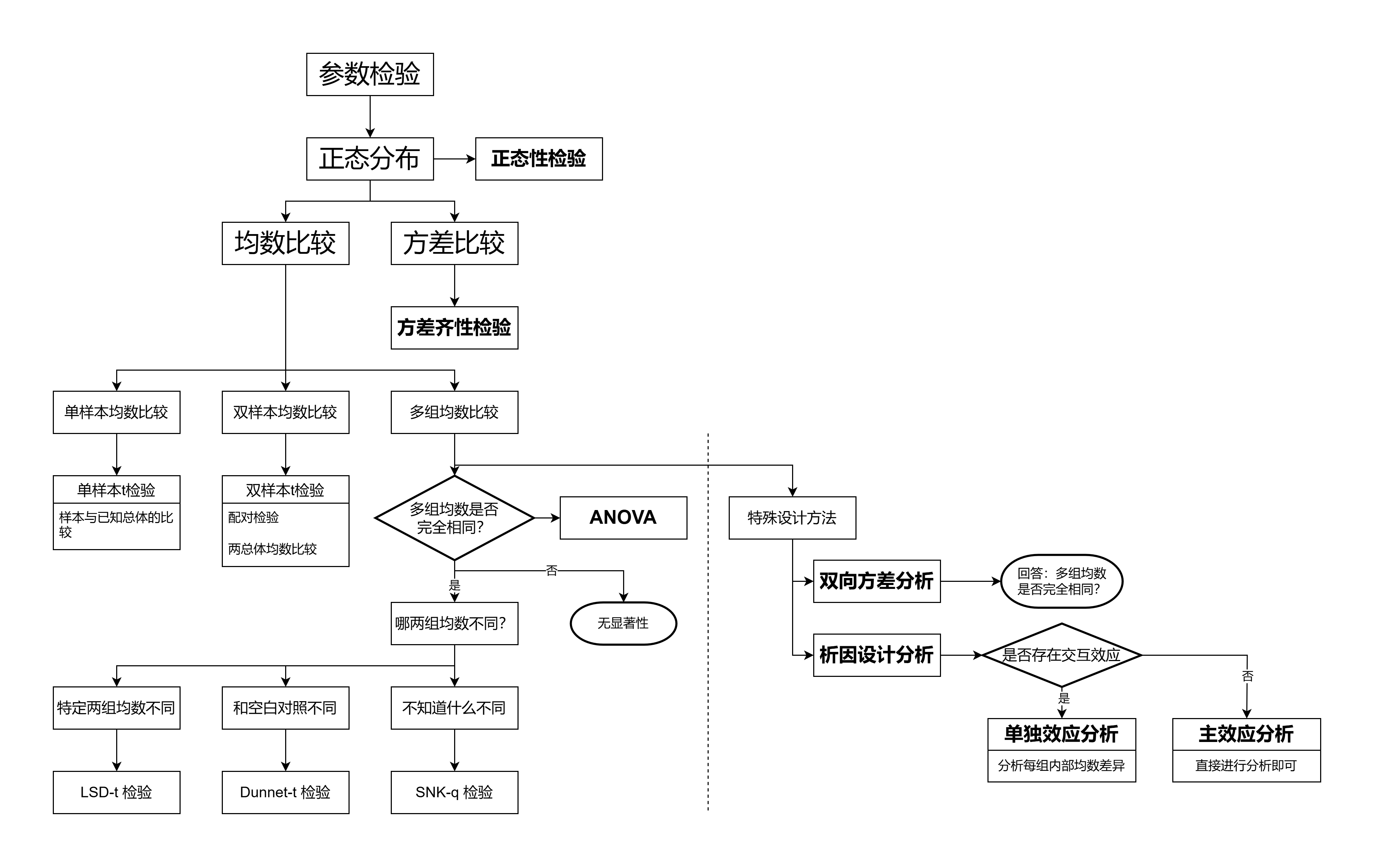
循证医学5-6周回顾
ANOVA
多组样本均数比较
多重比较
SNK-Q, Dunnet-t, LSD-t检验，其中SNK-q最难显著，LSD-t最容易显著
SNK-q: 任意两组进行均数的比较
Dunnet-t: k-1个实验组与一个对照组的比较
LSD-t: 特定几组的比较
前提
正态分布
方差齐性
Bartlett检验： 服从正态分布
Levene检验：服从任意分布
双向方差分析
方差分析不等于分析方差，方差分析分析均数
类似于ANOVA,仅可以做到比较多组是否全部相同。
析因设计的方差分析
先确定有无交互效应
若无交互效应则进行主效应分析
若有交互效应则进行单独效应分析
F&Q: 老师上课所使用的单变量回归该如何理解？单变量回归的作用是不是就是将不同正态分布的总体拉到同一基线上？
对于析因设计的方差检验，由于数据内部存在多组正态分布，导致数据总体不满足正态分布，所以需要分析其拟合后残差是否满足正态性与方差齐性
$$
\begin{aligned}
Y = \beta_{0} + \beta_{1} X_{1} + \beta_{2}X_{2}
\end{aligned}$$
如果$X_{1}$: 肝脏=0，心脏=1；$X_{2}$: 15min=0，60min=1；$Y$: 药物浓度
如果我们研究不同时间的药物浓度是否相同:
$$
\begin{aligned}
Y = \beta_{0} + \beta_{2}X_{2}\
Y - \beta_{1} = \beta_{0}+\beta_{2}X_{2}
\end{aligned}$$
上面第一个式子是肝脏的药物浓度、第二个式子是心脏的药物浓度，但是我们给心脏的药物浓度做了个”修正”, 这个时候两数据的均值其实就”对齐”了
二项分布
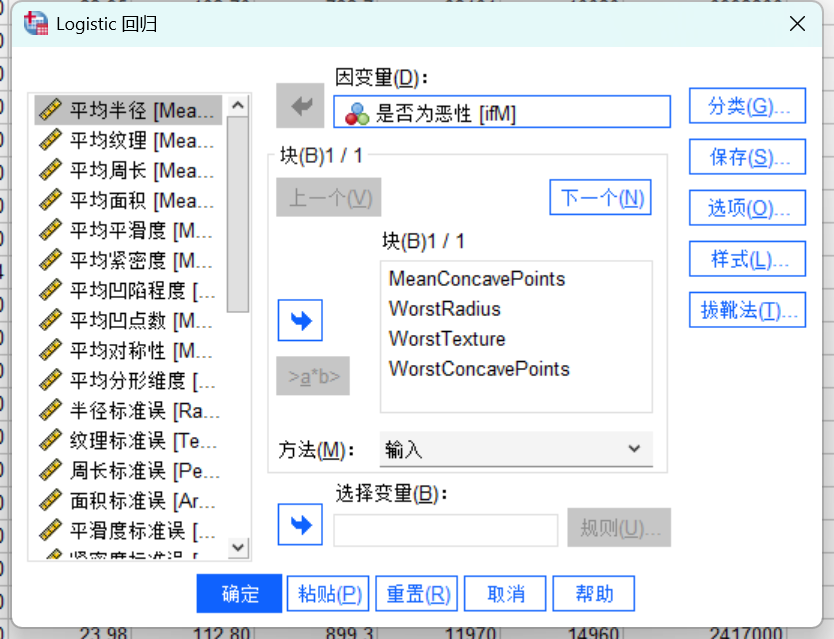
如果我们的数据不满足正态分布，而是满足二项分布，那我们该如何进行分析？
广义线性模型
Cover image icon by Freepik from Flaticon
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Evanescence's Blog！
相关推荐
2025-05-06
循证医学1-2周回顾
第一周的主要内容其实就是意识到概率论和数理统计之间的关系 统计学中的基本概念PPT-1基本概念总体——参数——$\mu, \sigma$样本——统计量——$\bar{X}, \bar{Y}$同质性与异质性抽样误差(sampling error) 计量资料——有序计数资料——有序等级资料——无序 因果与联系：金字塔顶端RCT研究，RCT是揭示事物因果关系最重要的方法，但是由于价格原因，大部分时间只能使用他的替代方案。 抽样误差的有趣知识SE为什么要有SE？如下图所示，美国为了研究班级人数的多少和班级平均分的关系，他们发现分数高的是那些班级人数较少的班级，但事实上，只是因为班级人数过少导致SE增大带来的错误因果！ PPT-2不同均数的适应情况，及为什么适应： 算术均数算术均数适用于正态分布，因为算术均数其实是正态分布的通过极大似然估计得到的均值$$P(x)=\frac{1}{\sqrt{ 2\pi...
2025-05-06
循证医学3-4周回顾
假设检验 检验的对象：抽样样本的均值，均值分布满足正态分布、抽样所得样本不一定满足正态分布 从正态分布——u分布——t分布(方差未知时用，大部分时候) 可信区间的计算(CI)：依赖于标准正态分布$\mathcal{N}(0,1)$ ,双边检验和单边检验的区分变换方法：$$\begin{aligned}X \sim \mathcal{N}(\mu, \sigma^2)\\X-\mu \sim \mathcal{N}(0, \sigma^2)\\\frac{X-\mu}{\sigma} \sim \mathcal{N}(0, 1)\end{aligned}$$ 两组均数比较的参数检验单样本t检验和已知的均值比较。假设我检测的样本均值为$\bar{X} \sim \mathcal{N}(\mu_{1}, \frac{\sigma_{1}^2}{n})$，总体均值为常数$\mu_{2}$，然后我们对这两个作差得到:$$\bar{X}-\mu_{2}\sim \mathcal{N}(\mu_{1}-\mu_{2},...
2025-05-06
循证医学7-8周回顾
二项分布与poisson分布及其应用二项分布 $$ P(X) = C^x_{n} \pi^x (1-\pi)^{n-x}$$ $$\mu = n\pi, \sigma^2={ n\pi(1-\pi) }$$ 样本率的方差计算同正态分布时的均值的方差计算：$$S_{p}=\sqrt{ \frac{p(1-p)}{n} }$$总体率置信区间计算： 查表方法 正态近似法(样本容量>100, $\pi \approx 0.5$) $$\begin{aligned} u &= \frac{{p-\pi_{0}}}{\sigma_{p}} \\ \sigma_{p} &= \sqrt{ \frac{\pi_{0}(1-\pi_{0})}{n} } \end{aligned}$$ *既往死亡率为40%，实验中120名病人死亡30名，统计推断： H_0: 均值不等 H_1: 均值相等 确定alpha值为0.05，双尾检验* $$\begin{aligned} \sigma_{p}&=\sqrt{ \frac{\pi_{0}(1-\pi_{0})}{n}...
2025-05-10
循证医学9-12周回顾
非参数检验非参数检验的适应条件 等级顺序资料 偏态资料 未知分布资料 各组资料的变异度大，方差不齐，变换也不能达到齐性 数据一端或两端有不确定值的资料 初步分析可以举几个例子：1. 不满足参数检验的要求；2. 血糖水平高于最高值会显示high 非参数检验的缺点容易出现第II类错误，即假阴性概率增大，本应显示出显著性差异的结果但是却并没有出现显著性差异。 两组配对设计资料的比较Wilcoxon符号秩和检验 符号检验 配对设计差值的符号秩检验：其实就是对差值进行符号检验 单样本资料的符号秩和检验Wilcoxon符号秩和检验。对标单样本正态检验 成组设计两样本比较的秩和检验Wilcoxon秩和检验 成组设计多个样本比较的秩和检验Kruskal Wallis H检验 原始数据的多个样本比较对标参数检验中的ANOVA，用于揭示多组数据的中位数是否完全相同 多个样本两两比较的秩和检验对标参数检验中的SNK-Q,...
