循证医学1-2周回顾
第一周的主要内容其实就是意识到概率论和数理统计之间的关系
统计学中的基本概念
PPT-1
基本概念
总体——参数——$\mu, \sigma$
样本——统计量——$\bar{X}, \bar{Y}$
同质性与异质性
抽样误差(sampling error)
计量资料——有序
计数资料——有序
等级资料——无序
因果与联系:
金字塔顶端RCT研究,RCT是揭示事物因果关系最重要的方法,但是由于价格原因,大部分时间只能使用他的替代方案。
抽样误差的有趣知识SE
为什么要有SE?
如下图所示,美国为了研究班级人数的多少和班级平均分的关系,他们发现分数高的是那些班级人数较少的班级,但事实上,只是因为班级人数过少导致SE增大带来的错误因果!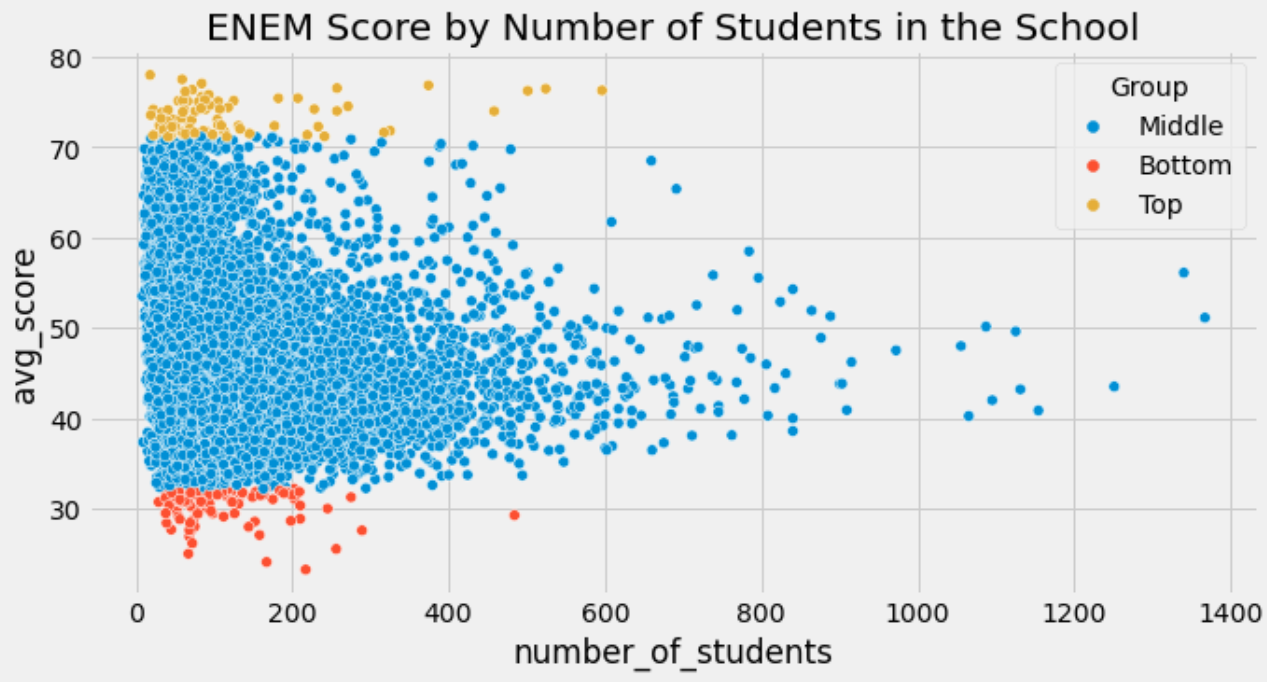
PPT-2
不同均数的适应情况,及为什么适应:
算术均数
算术均数适用于正态分布,因为算术均数其实是正态分布的通过极大似然估计得到的均值
$$P(x)=\frac{1}{\sqrt{ 2\pi }\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
$$\begin{aligned}
l(x_{1},x_{2},\dots,x_{n})&=\sum_{i=1}^n \ln P(x_{i})\\
&=\sum_{i=1}^n (\ln \frac{1}{\sqrt{ 2\pi }\sigma} + \ln e^{-\frac{(x_{i}-\mu)^2}{2\sigma^2}})\\
&=\sum_{i=1}^n (\ln \frac{1}{\sqrt{ 2\pi }\sigma} -\frac{(x_{i}-\mu)^2}{2\sigma^2})
\end{aligned}$$
求使上式子最大的$\mu$
$$\frac{dl}{d\mu}=\sum_{i=1}^n \frac{x_{i}-\mu}{\sigma^2}=0$$
so
$$\mu=\frac{1}{n}\sum_{i=1}^n x_{i}$$
几何均数
几何均数适用于对数转换后呈正态分布的资料,即右偏态
存在部分数值特别大的
为什么使用几何均数?
为什么能用累乘解释:
比如,某机械厂生产机器,设有毛坯、粗加工、精加工和装配4个连续作业的车间。某批产品其毛坯车间制品合格率为97%,接下来3个车间的合格率分别为93%、91%和87%,求产品的平均合格率。
产品的平均合格率受制于4个车间的坏品或损耗情况,由于是连续作业的车间,所以是在前者基础上变成了百分之多少的感觉,符合几何平均数的应用。
直接使用几何平均数的公式,计算得出:
$$G=(0.97 \times 0.93 \times 0.91 \times 0.87)^{1/4}=0.9193$$
中位数
$$M=L_{M}+\frac{i_{M}}{f_{M}}\left( \frac{n}{2} -\sum f_{L}\right)$$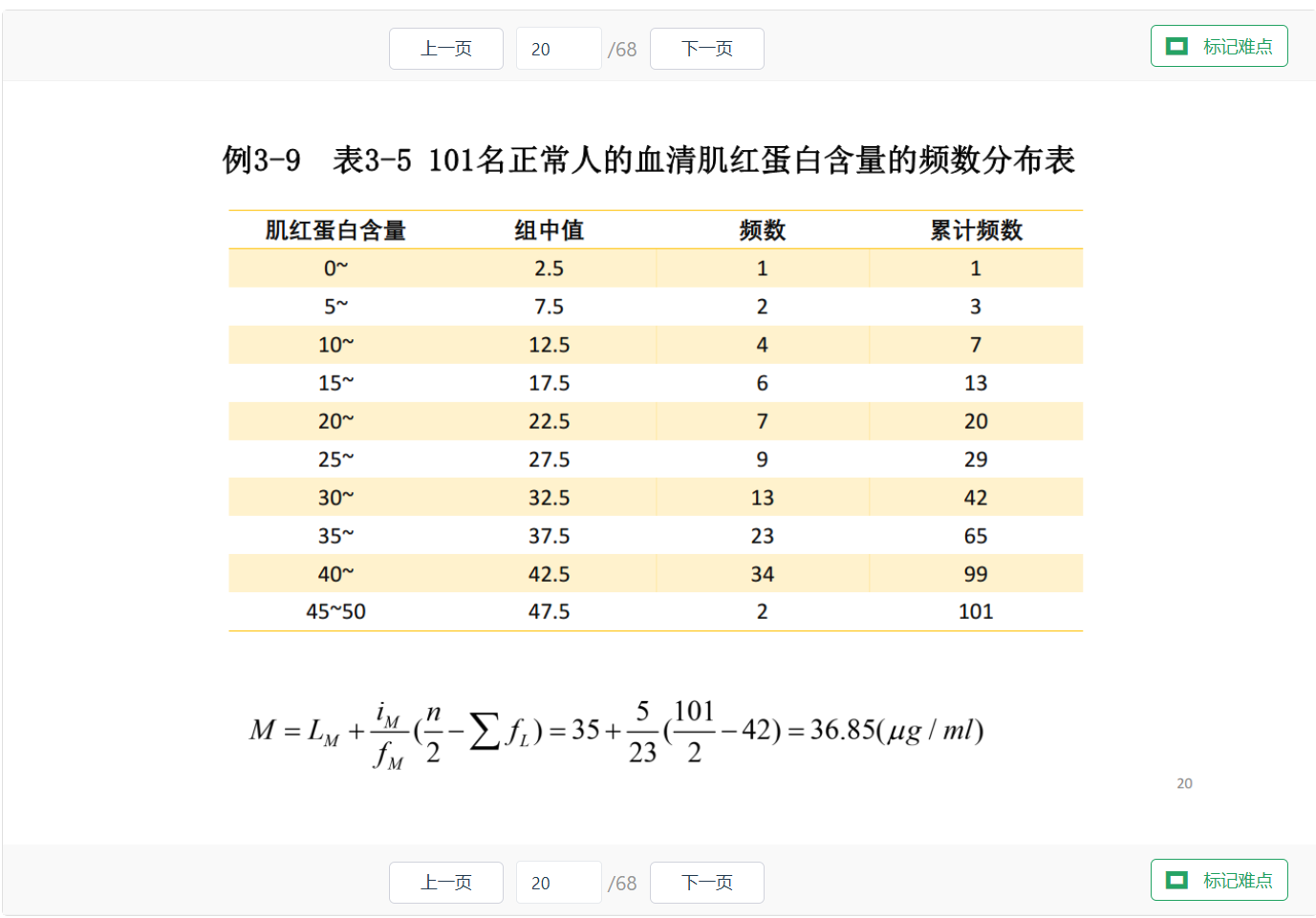
标准差
为什么会有一个$\sigma$和$S$
而且$S$下面的分母为$n-1$
这是因为在计算均数时已经消耗掉一个自由度,所以需要减去一个自由度。通俗的讲,均数其实是偏向于我们采样的数据,所以在计算方差时需要让除数小一点,这样让方差更大,更加接近真实方差。
总结
正态分布: 能使用算术均数和标准差描述
右偏态数据使用: 几何均数
所有分布都可以使用的: 众数、四分位数间距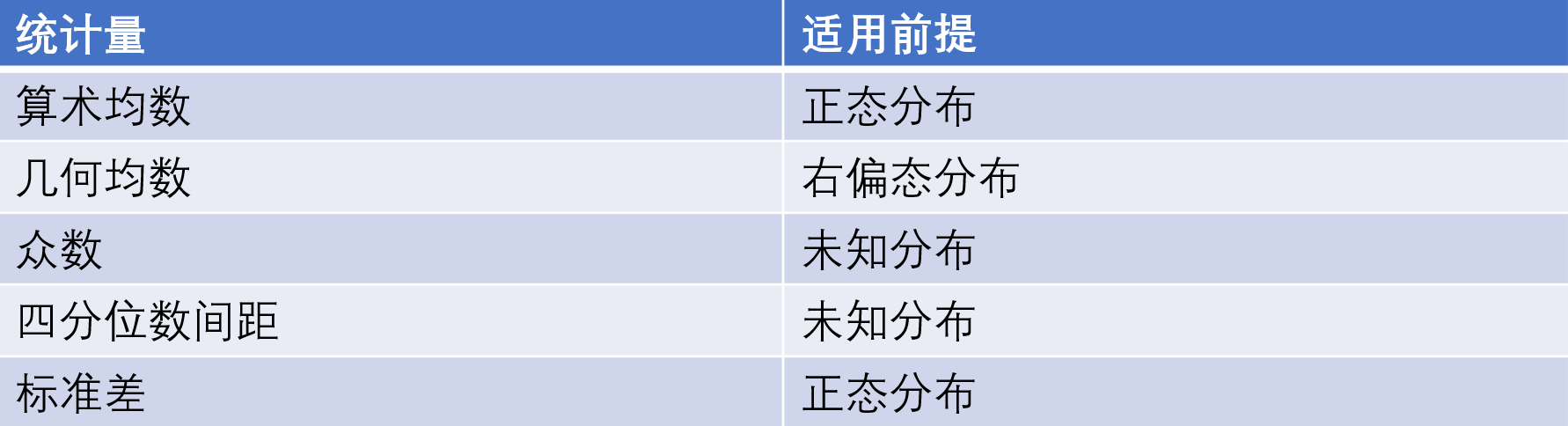
Cover image icon by Freepik from Flaticon

